Regression Code Snippets
This is how we ran our linear regression model. Attached is our code and full model results:
import pandas as pd
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
from sklearn.metrics import r2_score
# Load the datasets using the given file paths
zip_sea = pd.read_csv('inputs/zip_sea.csv')
zip_sea_new = pd.read_csv('inputs/zip_sea_new.csv')
# Replace missing values with NaN
zip_sea['Price'] = pd.to_numeric(zip_sea['Price'], errors='coerce')
zip_sea_new['Price'] = pd.to_numeric(zip_sea_new['Price'], errors='coerce')
# Create the model formula
formula = 'Price ~ GMSL_noGIA * Q("Inland/Coastal") + C(Pair)'
# Create and fit the model using the training set (zip_sea.csv)
model = smf.ols(formula, data=zip_sea).fit()
# Evaluate the model using the testing set (zip_sea_new.csv) and calculate the R-squared score
zip_sea_new['PredPrice'] = model.predict(zip_sea_new)
# Save the predictions to a file called predict.csv in the outputs folder
zip_sea_new.to_csv('outputs/predict.csv', index=False)
# Output the model summary
print(model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: Price R-squared: 0.875
Model: OLS Adj. R-squared: 0.874
Method: Least Squares F-statistic: 824.4
Date: Wed, 03 May 2023 Prob (F-statistic): 0.00
Time: 03:09:14 Log-Likelihood: -63939.
No. Observations: 4739 AIC: 1.280e+05
Df Residuals: 4698 BIC: 1.282e+05
Df Model: 40
Covariance Type: nonrobust
==================================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------------------------
Intercept 2.204e+05 1.86e+04 11.879 0.000 1.84e+05 2.57e+05
C(Pair)[T.2] -1.797e+05 2.31e+04 -7.791 0.000 -2.25e+05 -1.34e+05
C(Pair)[T.3] 7809.4521 2.17e+04 0.359 0.719 -3.48e+04 5.04e+04
C(Pair)[T.4] 4.27e+05 2.34e+04 18.227 0.000 3.81e+05 4.73e+05
C(Pair)[T.5] 5.118e+05 2.09e+04 24.476 0.000 4.71e+05 5.53e+05
C(Pair)[T.6] 2.658e+06 2.4e+04 110.636 0.000 2.61e+06 2.71e+06
C(Pair)[T.7] -5.444e+04 2.22e+04 -2.451 0.014 -9.8e+04 -1.09e+04
C(Pair)[T.8] -672.3418 1.96e+04 -0.034 0.973 -3.91e+04 3.78e+04
C(Pair)[T.9] -3.692e+04 1.99e+04 -1.852 0.064 -7.6e+04 2152.773
C(Pair)[T.10] -6.049e+04 1.96e+04 -3.082 0.002 -9.9e+04 -2.2e+04
C(Pair)[T.11] -6.696e+04 2.07e+04 -3.235 0.001 -1.08e+05 -2.64e+04
C(Pair)[T.12] 1.469e+05 3.25e+04 4.513 0.000 8.31e+04 2.11e+05
C(Pair)[T.13] 1.723e+05 2.29e+04 7.521 0.000 1.27e+05 2.17e+05
C(Pair)[T.14] 1.68e+05 2.07e+04 8.132 0.000 1.27e+05 2.08e+05
C(Pair)[T.15] 3.706e+04 2.09e+04 1.772 0.076 -3939.019 7.81e+04
C(Pair)[T.16] 7.841e+04 2.2e+04 3.557 0.000 3.52e+04 1.22e+05
C(Pair)[T.17] -5.26e+04 2.34e+04 -2.245 0.025 -9.85e+04 -6672.796
C(Pair)[T.18] -6.673e+04 2.06e+04 -3.241 0.001 -1.07e+05 -2.64e+04
C(Pair)[T.19] 1.351e+05 2.25e+04 5.999 0.000 9.09e+04 1.79e+05
C(Pair)[T.20] -8712.1662 3.04e+04 -0.286 0.775 -6.84e+04 5.1e+04
C(Pair)[T.21] -4.863e+04 2.65e+04 -1.833 0.067 -1.01e+05 3389.615
C(Pair)[T.22] -1.392e+05 1.96e+04 -7.094 0.000 -1.78e+05 -1.01e+05
C(Pair)[T.23] 3.206e+04 2.34e+04 1.369 0.171 -1.39e+04 7.8e+04
C(Pair)[T.24] -8.923e+04 2.11e+04 -4.235 0.000 -1.31e+05 -4.79e+04
C(Pair)[T.25] -6.56e+04 2.1e+04 -3.119 0.002 -1.07e+05 -2.44e+04
C(Pair)[T.26] -7.601e+04 2.27e+04 -3.348 0.001 -1.21e+05 -3.15e+04
C(Pair)[T.27] -1.339e+05 2.21e+04 -6.058 0.000 -1.77e+05 -9.06e+04
C(Pair)[T.28] 1.993e+05 1.96e+04 10.155 0.000 1.61e+05 2.38e+05
C(Pair)[T.29] 2.844e+04 1.96e+04 1.449 0.147 -1e+04 6.69e+04
C(Pair)[T.30] -5.922e+04 2.06e+04 -2.881 0.004 -9.95e+04 -1.89e+04
C(Pair)[T.31] 1.721e+05 2.05e+04 8.385 0.000 1.32e+05 2.12e+05
C(Pair)[T.32] 1.699e+05 2.07e+04 8.221 0.000 1.29e+05 2.1e+05
C(Pair)[T.33] 3.953e+05 2.37e+04 16.653 0.000 3.49e+05 4.42e+05
C(Pair)[T.34] 2.142e+06 3.37e+04 63.654 0.000 2.08e+06 2.21e+06
C(Pair)[T.35] 2.165e+06 3.19e+04 67.920 0.000 2.1e+06 2.23e+06
C(Pair)[T.36] -6.228e+04 2.25e+04 -2.766 0.006 -1.06e+05 -1.81e+04
C(Pair)[T.37] -4.811e+04 1.96e+04 -2.451 0.014 -8.66e+04 -9635.787
C(Pair)[T.38] -9.626e+04 1.96e+04 -4.905 0.000 -1.35e+05 -5.78e+04
GMSL_noGIA 1914.7325 357.292 5.359 0.000 1214.273 2615.192
Q("Inland/Coastal") 3318.4174 1.43e+04 0.232 0.816 -2.47e+04 3.13e+04
GMSL_noGIA:Q("Inland/Coastal") -1397.5213 471.366 -2.965 0.003 -2321.621 -473.422
==============================================================================
Omnibus: 3627.576 Durbin-Watson: 2.738
Prob(Omnibus): 0.000 Jarque-Bera (JB): 565488.120
Skew: -2.807 Prob(JB): 0.00
Kurtosis: 56.220 Cond. No. 1.23e+03
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.23e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
This code snippet is our second model with log(price) with full model results:
import pandas as pd
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
from sklearn.metrics import r2_score
# Load the datasets using the given file paths
zip_sea = pd.read_csv('inputs/zip_sea.csv')
zip_sea_new = pd.read_csv('inputs/zip_sea_new.csv')
# Replace missing values with NaN
zip_sea['LogPrice'] = np.log(zip_sea['Price'])
zip_sea['LogPrice'] = zip_sea['LogPrice'].replace([np.inf, -np.inf], np.nan)
zip_sea_new['LogPrice'] = np.log(zip_sea_new['Price'])
zip_sea_new['LogPrice'] = zip_sea_new['LogPrice'].replace([np.inf, -np.inf], np.nan)
# Create the model formula
formula = 'LogPrice ~ GMSL_noGIA * Q("Inland/Coastal") + C(Pair)'
# Create and fit the model using the training set (zip_sea.csv)
model = smf.ols(formula, data=zip_sea).fit()
# Evaluate the model using the testing set (zip_sea_new.csv) and calculate the R-squared score
zip_sea_new['PredLogPrice'] = model.predict(zip_sea_new)
# Save the predictions to a file called predict.csv in the outputs folder
zip_sea_new.to_csv('outputs/predict2.csv', index=False)
# Output the model summary
print(model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: LogPrice R-squared: 0.913
Model: OLS Adj. R-squared: 0.912
Method: Least Squares F-statistic: 1229.
Date: Tue, 02 May 2023 Prob (F-statistic): 0.00
Time: 23:05:53 Log-Likelihood: 913.99
No. Observations: 4739 AIC: -1746.
Df Residuals: 4698 BIC: -1481.
Df Model: 40
Covariance Type: nonrobust
==================================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------------------------
Intercept 12.2859 0.021 581.278 0.000 12.244 12.327
C(Pair)[T.2] -1.1615 0.026 -44.208 0.000 -1.213 -1.110
C(Pair)[T.3] 0.0436 0.025 1.761 0.078 -0.005 0.092
C(Pair)[T.4] 0.9987 0.027 37.416 0.000 0.946 1.051
C(Pair)[T.5] 1.1253 0.024 47.229 0.000 1.079 1.172
C(Pair)[T.6] 2.3337 0.027 85.237 0.000 2.280 2.387
C(Pair)[T.7] -0.2521 0.025 -9.959 0.000 -0.302 -0.202
C(Pair)[T.8] 0.0260 0.022 1.164 0.245 -0.018 0.070
C(Pair)[T.9] -0.1237 0.023 -5.449 0.000 -0.168 -0.079
C(Pair)[T.10] -0.2398 0.022 -10.725 0.000 -0.284 -0.196
C(Pair)[T.11] -0.2685 0.024 -11.387 0.000 -0.315 -0.222
C(Pair)[T.12] 0.4100 0.037 11.058 0.000 0.337 0.483
C(Pair)[T.13] 0.5224 0.026 20.013 0.000 0.471 0.574
C(Pair)[T.14] 0.5325 0.024 22.623 0.000 0.486 0.579
C(Pair)[T.15] 0.0772 0.024 3.239 0.001 0.030 0.124
C(Pair)[T.16] 0.2729 0.025 10.864 0.000 0.224 0.322
C(Pair)[T.17] -0.1946 0.027 -7.291 0.000 -0.247 -0.142
C(Pair)[T.18] -0.2768 0.023 -11.797 0.000 -0.323 -0.231
C(Pair)[T.19] 0.4216 0.026 16.437 0.000 0.371 0.472
C(Pair)[T.20] -0.0257 0.035 -0.741 0.459 -0.094 0.042
C(Pair)[T.21] -0.4239 0.030 -14.021 0.000 -0.483 -0.365
C(Pair)[T.22] -0.8296 0.022 -37.101 0.000 -0.873 -0.786
C(Pair)[T.23] 0.1453 0.027 5.444 0.000 0.093 0.198
C(Pair)[T.24] -0.4083 0.024 -17.010 0.000 -0.455 -0.361
C(Pair)[T.25] -0.2813 0.024 -11.740 0.000 -0.328 -0.234
C(Pair)[T.26] -0.2783 0.026 -10.759 0.000 -0.329 -0.228
C(Pair)[T.27] -0.7947 0.025 -31.555 0.000 -0.844 -0.745
C(Pair)[T.28] 0.6203 0.022 27.740 0.000 0.576 0.664
C(Pair)[T.29] 0.1433 0.022 6.411 0.000 0.100 0.187
C(Pair)[T.30] -0.2231 0.023 -9.524 0.000 -0.269 -0.177
C(Pair)[T.31] 0.5375 0.023 22.986 0.000 0.492 0.583
C(Pair)[T.32] 0.5487 0.024 23.306 0.000 0.503 0.595
C(Pair)[T.33] 0.9426 0.027 34.853 0.000 0.890 0.996
C(Pair)[T.34] 2.2364 0.038 58.316 0.000 2.161 2.312
C(Pair)[T.35] 2.2438 0.036 61.776 0.000 2.173 2.315
C(Pair)[T.36] -0.2164 0.026 -8.433 0.000 -0.267 -0.166
C(Pair)[T.37] -0.1813 0.022 -8.107 0.000 -0.225 -0.137
C(Pair)[T.38] -0.4553 0.022 -20.361 0.000 -0.499 -0.411
GMSL_noGIA 0.0045 0.000 11.148 0.000 0.004 0.005
Q("Inland/Coastal") -0.0131 0.016 -0.803 0.422 -0.045 0.019
GMSL_noGIA:Q("Inland/Coastal") 0.0005 0.001 0.956 0.339 -0.001 0.002
==============================================================================
Omnibus: 387.415 Durbin-Watson: 2.625
Prob(Omnibus): 0.000 Jarque-Bera (JB): 2239.378
Skew: -0.117 Prob(JB): 0.00
Kurtosis: 6.359 Cond. No. 1.23e+03
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.23e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
This is when we combine the predictions from both models to better compare model accuracy:
import csv
# Read data from predict.csv
with open('outputs/predict.csv', 'r') as csvfile1:
csvreader1 = csv.reader(csvfile1)
predict_data = [row for row in csvreader1]
# Read data from predict2.csv
with open('outputs/predict2.csv', 'r') as csvfile2:
csvreader2 = csv.reader(csvfile2)
predict2_data = [row for row in csvreader2]
# Combine the last column of predict2.csv into predict.csv
for i in range(len(predict_data)):
if i == 0:
predict_data[i].extend(["PredLogPrice"])
else:
predict_data[i].append(predict2_data[i][-1])
# Write the combined data to a new CSV file
with open('outputs/combined_predict.csv', 'w', newline='') as csvfile:
csvwriter = csv.writer(csvfile)
csvwriter.writerows(predict_data)
print("Combined data saved to 'combined_predict.csv'")
Combined data saved to 'combined_predict.csv'
Please see below for our prediction visualizations:
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# Load the combined_data.csv file
combined_data = pd.read_csv("outputs/combined_predict.csv")
combined_data['LogPredPrice'] = np.log(combined_data['PredPrice'])
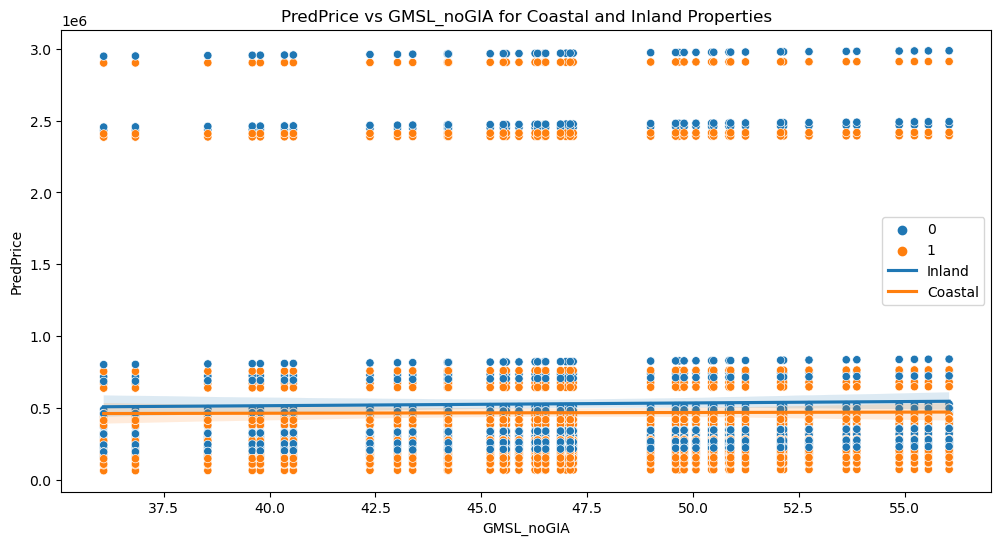
# Scatterplot with PredPrice
plt.figure(figsize=(12, 6))
sns.scatterplot(x="GMSL_noGIA", y="PredPrice", hue="Inland/Coastal", data=combined_data)
plt.title("PredPrice vs GMSL_noGIA for Coastal and Inland Properties")
# Add linear regression lines
coastal_data = combined_data[combined_data["Inland/Coastal"] == 1]
inland_data = combined_data[combined_data["Inland/Coastal"] == 0]
sns.regplot(x="GMSL_noGIA", y="PredPrice", data=inland_data, scatter=False, label="Inland")
sns.regplot(x="GMSL_noGIA", y="PredPrice", data=coastal_data, scatter=False, label="Coastal")
plt.legend()
plt.savefig('graphs/predprice_vs_GMSL_noGIA_coastal_inland.png', dpi=300, bbox_inches='tight')
plt.show()
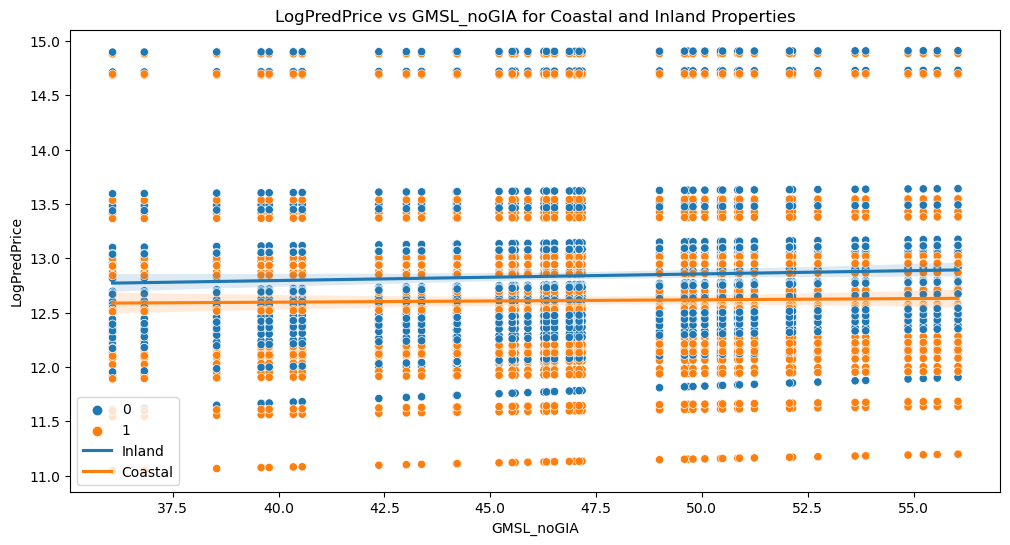
# Scatterplot with LogPredPrice
plt.figure(figsize=(12, 6))
sns.scatterplot(x="GMSL_noGIA", y="LogPredPrice", hue="Inland/Coastal", data=combined_data)
plt.title("LogPredPrice vs GMSL_noGIA for Coastal and Inland Properties")
# Add linear regression lines
sns.regplot(x="GMSL_noGIA", y="LogPredPrice", data=inland_data, scatter=False, label="Inland")
sns.regplot(x="GMSL_noGIA", y="LogPredPrice", data=coastal_data, scatter=False, label="Coastal")
plt.legend()
plt.savefig('graphs/logpredprice_vs_GMSL_noGIA_coastal_inland.png', dpi=300, bbox_inches='tight')
plt.show()